How to calculate the PV value for a lead screw application

Lead screws rely on sliding friction between the nut and the screw to convert rotary motion into axial (thrust) force to move a load. Most lead screw designs use either a carbon steel screw with a bronze nut, or a stainless steel screw with a plastic nut. In either case, there are no recirculating balls or rollers, so the typical method of calculating expected service life—the L10 bearing life equation—doesn’t apply. Instead, manufacturers use a combination of empirical testing, real-world experience, and technical factors to estimate the expected life.

For lead screws with plastic nuts, one of these factors is the PV rating. The PV rating is the highest combination of pressure (P) and velocity (V) that the screw and nut can withstand, based on the heat generated by the screw and nut surfaces sliding against one another. Checking the PV value of an application against the PV rating of the screw and nut is an important step in selecting a lead screw assembly.

Pressure

In the PV equation, pressure is simply the axial load divided by the contact area between the nut and the screw.

P = pressure between screw and nut (MPa or psi)

F_A = axial load on the nut (N or lb)

A = area of contact (m² or in²)

However, finding the contact area for a helical mechanism, such as a lead screw, is more complicated than for a cylindrical design, such as linear bushing and shaft assembly. In the case of a lead screw assembly, the contact area equals the helix length multiplied by the depth of engagement between the screw and the nut.

l_h = helix length (m or in)

d_t = depth of engagement (m or in)

But plastic nuts tend to flex and bend when a load is applied, which reduces the contact area and increases the pressure, so some manufacturers recommend multiplying the contact area by a correction factor (typically between 0.75 and 0.25).

C_f = correction factor for reduced area

To find the helix length, the thread can be “unwrapped” to form a right triangle, with the helix length as the hypotenuse, the lead as the upright side, and the pitch diameter as the base. Solving for the hypotenuse of the triangle gives us the helix length per revolution.

l_hr = helix length per revolution (m or ft)

L = screw lead (m or ft)

D_p = screw pitch diameter (m or ft)

To find the total helix length, multiply the helix length per rotation by the number of thread turns (nut length divided by screw lead) and by the number of starts (if using a multi-start nut).

l_h = total helix length (m or in)

l_n = nut length (m or in)

L = screw lead (m or in)

S_t = number of starts

The depth of engagement is found by subtracting the screw’s root diameter from its outer diameter.

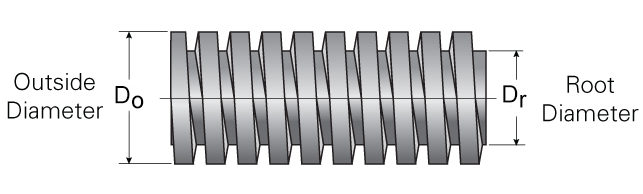
D_o = screw outer diameter (m or in)

D_r = screw root diameter (m or in)

Velocity

Remember that the PV value is based on friction and heat generation between the screw and the nut, so when evaluating the velocity component, we need to determine the linear velocity between the screw and the nut. This is done by multiplying the rotational speed by the helix length per revolution.

V= linear velocity between screw and nut (m/s or fpm)

Notice that the velocity is given in units of either meters per second (m/s) or feet per minute (fpm). When calculating the linear velocity for the PV value, double check to be sure that you’ve made any necessary conversions for both the length units (inches to feet, or millimeters to meters) and the time units (minutes or seconds).

Feature image credit: AMETEK Inc.