When designing and sizing a linear motion system, one of the first steps is to determine what type of move profile the application requires, since this determines how to calculate velocity and acceleration, and has a significant effect on their average and maximum values.
Velocity and acceleration are two fundamental aspects of any linear motion application. They affect the forces on the guide system, the torque required by the drive components, and in some cases, they immediately narrow the choice of guides and drives that can be considered. Case in point: if your application calls for 5 m/s maximum speed, a ball or lead screw is probably out of the question, and you’ll need to look at a belt, rack and pinion, or linear motor drive.
The two fundamental move profiles, on which even the most complex processes are based, are triangular and trapezoidal, so named because of the shape of their velocity-time graph.
Triangular move profile
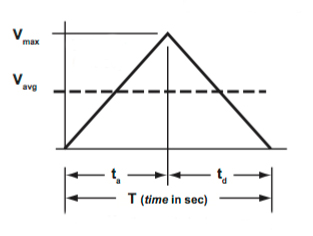
The basic premise of a triangular move profile is to accelerate to a maximum velocity, then immediately decelerate, with acceleration and deceleration being equal in terms of both time and distance. In other words, if you want to move from here to there in the fastest time, you would use a triangular move profile. Determining any of the move variables—time, velocity, acceleration, or distance—is based on the geometry of the triangle. Below are some common equations for triangular move profiles.
How to calculate average velocity
Since the acceleration and deceleration time are equivalent, and there is no constant velocity time, average velocity is simply total distance over total time:
![]()
How to calculate maximum velocity
Maximum velocity is the height, or peak, of the triangle, and is twice the average velocity:
![]()
How to calculate acceleration
Acceleration is the slope of one side of the triangle (“rise over run”). This is the maximum velocity divided by the acceleration time, which is half of the total move time:
![]()
Where ta = ½ tt
How to calculate total distance
The distance traveled equals the area under the curve. Since the curve is a triangle, distance equals the area of the triangle, or ½ * base * height. Thus, the total distance traveled equals ½ * total time (base) * maximum velocity (height), or:
![]()
How to calculate acceleration distance
Similarly for the distance traveled during acceleration (or deceleration, since they are equal), the area of the left (or right) half of the triangle is ½ * time to accelerate (base) * maximum velocity (height), or:
![]()
In addition to being the overall fastest option for getting from one point to the other, a triangular move profile requires lower acceleration than a trapezoidal profile, which translates to lower thrust forces on the drive unit.
Trapezoidal move profile
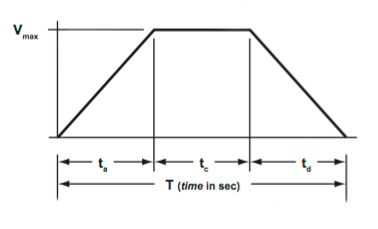
A trapezoidal move profile is used when the application needs to accelerate to a maximum velocity and then travel at that velocity for a specified time or distance. Some common processes that use trapezoidal move profiles are machining, dispensing, and painting.
The simplest form of trapezoidal move profile, and the one used in the examples below, is the 1/3, 1/3, 1/3 profile. In this case, 1/3 of the time is used for accelerating, 1/3 is used for constant velocity, and 1/3 is used for decelerating. But if you understand the geometry of the move profile, which is essentially two triangles and a rectangle, you can calculate the necessary parameters regardless of whether the time segments are equal or not.
How to calculate total distance
Recall from the triangular move profile discussion that distance traveled is equal to the area under the curve. The trapezoidal move profile can be treated as three curves, or segments: acceleration (triangle), constant velocity (rectangle), and deceleration (triangle). Therefore, the total distance traveled is the sum of the areas of the three curves:
![]()
Now, inserting the formulas for area of a triangle, rectangle, and another triangle:
![]()
In each segment, time represents the base, and maximum velocity represents the height, so we get:
![]()
Rearranging gives us:
![]()
For the 1/3, 1/3, 1/3 profile, ta = tc = td, and each segment equals 1/3 of the total time, tt. Thus, the equation becomes:
![]()
And simplifying, we get:
![]()
How to calculate maximum velocity
If maximum velocity needs to be determined, this equation can be rearranged to give:
![]()
Which can also be expressed as:
![]()
How to calculate average velocity
Like the triangular move profile, average velocity for a trapezoidal move profile is simply the total distance divided by the total time:
![]()
How to calculate acceleration
Because the middle segment (rectangle) is only for constant velocity (zero acceleration), the acceleration can be determined much the same way as for a triangular move profile. In this case, use either the left side triangle (for acceleration) or the right side triangle (for deceleration):
![]()
An equation based on distance and time can be derived if we substitute the vmax formula from above and insert 1/3tt for ta:
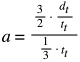
Simplified, acceleration can be expressed as:
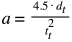
For applications that benefit from a period of constant velocity, a trapezoidal move profile offers the advantage of having a lower maximum velocity than a triangular profile.
While there are many variations on the triangular and trapezoidal move profiles, understanding their geometry and equations will help you solve just about any version that you may encounter.
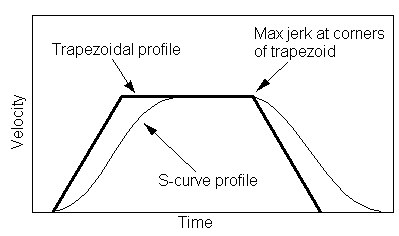
S-curve move profile: In real-world applications, true trapezoidal move profiles are rarely used, because of a phenomenon referred to as jerk. Just as acceleration is the rate of change of velocity, jerk is the rate of change of acceleration. Hence, in a trapezoidal move profile, when acceleration begins or ends, jerk is infinite. This leads to oscillations, which increases settling time and decreases positioning accuracy. The method for reducing jerk is to smooth the transitions where acceleration begins or ends, making the sharp corners of the trapezoidal profile more “s”-like.
If you’re not done calculating, check out our list of engineering calculators.




This is some great basic information on how to calculate the expected motion profile of a servo axis!