
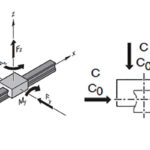
In linear guides and ball screws, load-carrying balls or rollers can ride on planar (flat) raceways, as with non-recirculating linear roller bearings, or in curved raceways, as with ball screws and profiled rail guides.
When a ball or roller rides on a planar raceway, the contact between the rolling element and the raceway will be very close to a point (for balls) or a line (for rollers). However, when a ball or roller rides in a curved raceway, the rolling element makes contact with the raceway at multiple locations and produces small areas of contact.
The location and shape of these areas of contact are determined by the conformity between the rolling element and the raceway.
Ball conformity is the dimensional relationship between the radius of the raceway and the diameter of the ball (or roller). A “perfect” fit between ball and raceway would be a conformity of 0.5, meaning the radius of the raceway is ½ the size of the ball diameter.

![]()
f = conformity
r = radius of raceway (mm)
D = diameter of ball (mm)
Although a conformity of 0.5 provides optimal load carrying capacity, it can lead to high differential slip (sliding) of the ball, so linear guides and screws are typically designed with a ball conformity between 0.51 and 0.54.
In ball screw assemblies, the raceway on the screw shaft has a different radius than the raceway inside the ball nut housing. Therefore, there are two measures of conformity for ball screws:
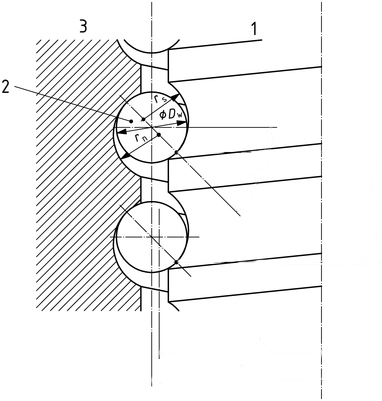
2 – ball
3 – ball nut
Image credit: ISO
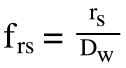
frs = conformity between ball and screw shaft
rs = radius of screw shaft raceway (mm)
Dw = diameter of ball (mm)
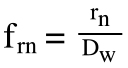
frn = conformity between ball and nut housing
rn = radius of nut housing raceway (mm)
Dw = diameter of ball (mm)
The amount of conformity is closely tied to the amount of Hertz contact stress that a ball (or roller) experiences under load, and ball conformity is one of the variables on which the Lundberg Palmgren bearing life theory is based. Ball conformity is also one of the factors that led to the development of profiled rail guides.
The first widely used recirculating bearings were linear ball bearings on round shafts. It was eventually discovered that by machining conformal grooves along the length of the shaft, the bearings could support higher loads (and transfer torque). Hence, the ball spline was created.
The next step in the evolution of recirculating linear guides was to do away with the round shaft and use a square profile guide instead, for ease of supporting and mounting. So now we have profiled rail linear guides, which use conformal grooves (raceways) on each side of the rail, for high load capacity and high rigidity.
Linear ball bearings that ride on round shafts experience point contact — no conformity — between the balls and the shaft. However, the load plate inside the bearing housing is typically grooved, so that the balls experience conformity with the load plate. This significantly increases load capacity and bearing life.
Conformity is also an important factor in the effectiveness of lubrication. The small area of contact that arises when a ball or roller experiences conformity with its raceway results in very high contact pressure. This high contact pressure increases the viscosity of the lubrication, which improves the lubrication’s ability to support the load without being squeezed out of the small contact zone. And because the area of contact is relatively large — compared to point or line contact — conformal bearings experience less deflection than bearings that ride on planar surfaces and have no (or very little) conformity.
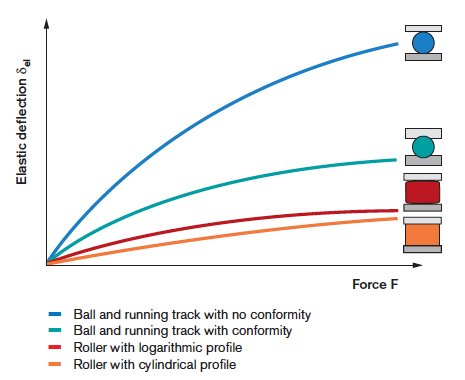
Image credit: Bosch Rexroth




Leave a Reply
You must be logged in to post a comment.