Let’s answer the first question: What does RMS stand for? RMS, or root mean square, is a statistical term that is used for determining the mean (or average) of a set of values. It’s especially useful when the values vary as a function of time.
The technical definition of root mean square is the square root of the mean of all the squares in a sample. For example, to find the root mean square of a set of values, first square each of the values. Then add those squares together, and divide their sum by the number of values. This gives you the mean (average) of the squares. Finally, take the square root of the mean that you just calculated, and that will give you the root mean square of the values.
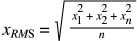
When the values are a function of time (which is the case in many linear motion and motion control applications), the equation for root mean square changes somewhat. Now, each value is squared and multiplied by its time factor. When the squared functions are summed, the result is divided by the total time of all the values.
One of the most common applications of root mean square in linear motion is RMS torque, which is a function of time because it varies over the course of the move profile (torque for acceleration, torque for holding a load, torque for standstill, etc.). Notice in the equation for RMS torque, shown below, that each torque value is multiplied by the time (t) for which that torque is applied, and the sum of the squares is divided by the total time of all the torque values (ttotal).
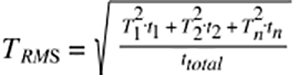
RMS torque is an important value because when a motor produces torque, it also produces heat. This is why the torque-speed curve of a motor typically includes two zones: a continuous duty zone, where the motor can produce the given range of torques and speeds continuously without overheating, and an intermittent zone, where the motor can only produce the range of torques and speeds for a short period of time before overheating occurs.
The maximum torque from the motor, which should fall within the intermittent zone of the torque-speed curve, is typically the sum of torque due to acceleration, torque due to the load, and torque due to friction. But because torque requirements vary throughout the duty cycle of the motor, the RMS torque value is used to determine the torque value that, if produced continuously by the motor, would result in the same amount of motor heating as all the various torques and durations that the motor actually sees during its duty cycle.
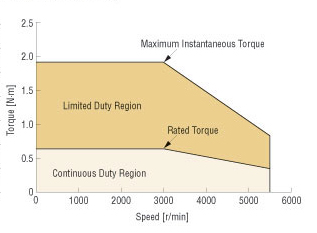
Image credit: Oriental Motor U.S.A. Corp.
Another application of root mean square in motion control is RMS current. If a servo motor is the muscle that makes a linear or rotary system move, then the servo drive is the nervous system, sending signals (in the form of current) that cause the motor to rotate. And in the same manner that producing torque causes heat to build up in a servo motor, producing current generates heat in a servo drive. Fortunately, calculating the RMS current is typically a more straightforward endeavor than calculating the RMS torque. RMS current is simply the RMS torque (TRMS) divided by the torque constant (KT) of the motor.
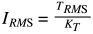
In linear motion systems, the root mean square calculation is useful for evaluating any parameter that varies with time, such as voltage, power, or velocity.





Leave a Reply
You must be logged in to post a comment.