When evaluating the accuracy of a linear motion system, the area of focus is often the positioning accuracy and repeatability of the drive mechanism. But there are many factors that contribute to the accuracy (or inaccuracy) of a linear system, including linear errors, angular errors, and Abbé errors. Of these three types, Abbé errors are probably the most difficult to measure, quantify, and prevent, but they can be the most significant cause of undesirable results in machining, measuring, and high-precision positioning applications.
Abbé errors begin as angular errors
Abbé errors are caused by the combination of angular errors in the motion system and the offset between the point of interest (tooling, load, etc.) and the origin of the error (screw, guideway, etc.).
Angular errors — commonly referred to as roll, pitch, and yaw — are unwanted motions due to the rotation of a linear system around its three axes.
If a system is moving horizontally along the X axis, as shown below, pitch is defined as rotation around the Y axis, yaw is rotation around the Z axis, and roll is rotation around the X axis.
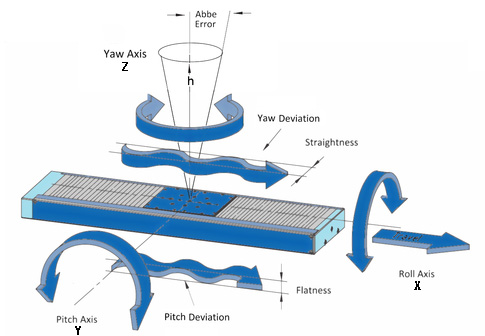
Image credit: PI USA
Errors in roll, pitch, and yaw typically result from inaccuracies in the guide system, but mounting surfaces and methods can also be sources of angular errors. For example, mounting surfaces that are not precisely machined, components that are not sufficiently fastened, or even varying rates of thermal expansion between the system and its mounting surface can all contribute to angular errors greater than those inherent in the linear guides themselves.

Abbé errors are especially problematic because they amplify what, in most cases, are very small angular errors, increasing in magnitude as the distance from the error-causing component (referred to as the Abbé offset) increases.
In the illustration to the right, the Abbé offset is h. The amount of Abbé error, δ, can be determined with the equation:
δ = h * tan θ
For overhung loads, the farther the load is from the cause of the angular error (typically the guideway or a point on the mounting surface), the higher the Abbé error will be. And for multi-axis configurations, Abbé errors are even more complex because they’re compounded by the presence of angular errors in each axis.
The best methods for minimizing Abbé errors are to use high-precision guides and to ensure that mounting surfaces are sufficiently machined so they don’t introduce additional inaccuracies to the system. Reducing the Abbé offset by moving the load as close as possible to the center of the system will also minimize Abbé errors.
Abbé errors are most accurately measured with a laser interferometer or other optical device that is completely independent of the system. But laser interferometers aren’t practical for most setups, so linear encoders are used in many applications where Abbé error is a concern. In this case, the most accurate measurements of Abbé error are achieved when the encoder read head is mounted on the point of interest — i.e. the tooling or the load.
XY tables are less susceptible to Abbé errors than other types of multi-axis systems (such as Cartesian robots) are, primarily because they minimize the amount of cantilevered travel and typically operate with the load located at the center of the Y axis carriage.





Leave a Reply
You must be logged in to post a comment.