by Jonathan R. Schroeder, Engineer

The Binding Ratio is a frequently misunderstood mechanical principle, with common misconceptions still causing stalling and application failure. A closer look at the mathematics behind the rule will give you a better comprehension of how to implement it.

One of the more frequently misunderstood principles regarding the use of plane bearings is something known simply as the 2:1 Ratio. Most engineers are taught there is this magic ratio (2:1) of allowable moment arm length to bearing length which cannot be violated or the application will fail.

The 2:1 Ratio was first introduced to the marketplace in the 1990s and has been adapted by most self-lubricating, linear-plane bearing manufacturers as one of the guiding principles regarding their use.

Plane bearing systems excel in many environments where recirculating ball-based systems failed; including very hot, cold or dirty environments; applications with high vibration or high static loads, and those with non-lubricated and short stroke (<2 x bearing length).

However, these bearings do not handle applications that require a low coefficient of friction, very high speeds or high moment loads. In fact, some applications with high moment loads simply bind up and cease all motion, or become jerky (also known as stick-slip motion).

Early on, the assumption was that plane bearings could not handle the same moment load as an equivalent sized recirculating ball bearing. What users failed to realize is that there was a geometric relationship that described the allowable working space of plane bearing—the 2:1 Ratio. Two decades later, some users still do not see the broad scope of this rule and that it applies to all linear motion systems, not just plane bearings.

In addition, the 2:1 Ratio isn’t always “2:1.” Depending upon the criteria of each application, the actual ratio may be larger or smaller than 2:1. For the purposes of this article, though, the 2:1 Ratio will be referred to as the “Binding Ratio.”

The “Binding Ratio” is officially defined as the maximum ratio of moment arm distance to bearing length, which will not bind (prevent motion). The Binding Ratio is often displayed numerically as “X:Y,” where “X” is the moment arm distance and “Y” is bearing length. Typically, the value of “X” is divided by “Y” so that the ratio can be expressed as “X/Y:1.”

While the binding ratio can be theoretically defined using mathematics, several factors complicate practical implementation.

One of the key principles is Sir Isaac Newton’s 3rd Law of Motion: for every action there is an equal and opposite reaction. The remainder breaks down to basic statics and dynamics equations. When a force is applied to a bearing at some distance (D₁) away from the center of the bearing, a moment force is created. In order to resist the moment, two resulting forces are created at each end of the bearing. When these resulting forces are multiplied by the Coefficient of Friction, a drag force is created. At some point the drag force will surpass the drive force and motion will cease.

The example will be where a single force (F₁) is applied to a linear bearing system at a known distance (D₁). Assuming the bearing system and moment arm are a rigid body, motion will be in the same direction that F₁ is applied. It can also be assumed that linear bearing systems are designed to allow only one degree of freedom; which is the axis of motion, Figure 1. Figure 2 shows the bearing with a force (F₁) applied to it at a known distance (D₁) as well as the length of the bearing (L₁). For the purposes of keeping these equations simple, an assumption is made that the applied force (F₁) is being applied in a single plane and is parallel to the direction of travel.

Figure 3 repeats the values shown in Figure 2, and then adds the equal and opposite reaction forces (F₂ and F₃); which are a result of the applied moment. Forces F₂ and F₃ are applied at points A and B, respectively.

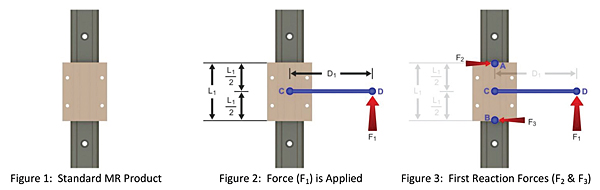
Figure 4 then shows the drag forces (F₄ and F₅), which are caused by the resulting forces (F₂ and F₃) multiplied by the coefficient of friction of the carriage versus the rail (μ) when the carriage is in motion.

Figure 5 shows the complete system and all forces acting upon the carriage.

Building upon Sir Isaac Newton’s 1st Law of Motion (an object at rest will stay at rest until the vectored sum of all forces acting upon it is greater than zero), in order for the carriage to accelerate, the applied force (F₁) must be greater than the sum of the drag forces (F₄ and F₅). In practice, there is an additional drag force due to the weight of the carriage plus the weight of the payload. For now, this additional resistance will be disregarded.

Equation 1: Acceleration (motion) > 0 → F₁ > F₄+ F₅

Equation 2:F₄ = μF₂ and F₅ = μF₃

Equation 3: Acceleration > 0 → F₁ > μF₂ + μF₃

Equation 4: Acceleration > 0 → F₁ > μ(F₂ + F₃)

To begin the statics equations, point C is chosen to be the fulcrum and all forces and moments are summed around this point. Figure 6 shows the lever arms resulting from the applied forces (F₁) and the resulting force (F₂ and F₃) with an origin of point C.

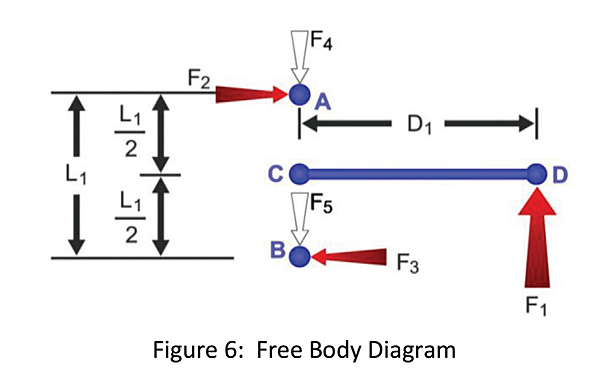
Since linear bearing systems are designed to be rotationally stable, it is known that the sum of the moments (about point C) is equal to zero (Equation 5). Equations 6 – 10 show the simplification of this equation in order to solve for the resulting forces F₂ and F₃.

Equation 5:  Rotationally Stable → ∑M_z = 0

Equation 6:  ∑M_z = 0 = (F₁ x D₁) – (F₂ x L₁/2) – (F₃ x L₁/2)

Equation 7:  (F₁ x D₁) = (F₂ x L₁/2) + (F₃ x L₁/2)

Equation 8:  (F₁ x D₁) = L₁/2 (F₂ + F₃)

Equation 9 : (2 x F1 x D1) /L1 = (F₂ + F₃)

At the transition point, where the bearing change from binding to motion (or vice-versa), the acceleration value from Equation 4 changes from a negative to a positive value. To solve for this, set the value to zero to find the specific transition point. The following group of equations is valid only at the transition point, where acceleration is equal to zero.

Equation 10: Acceleration = 0 → F₁ = μ(F₂+ F₃)

Equation 11: F₁ = μ ((2 x F₁ x D₁) / L₁ ) = (2 x μ x F₁ x D₁)/ L₁

Equation 12: (F₁ / F₁) = 1 = (2 x μ x D₁) / L₁

As mentioned before, for an application to be capable of motion, the driving force must be greater than the sum of the drag forces. Equation 12 shows that there is a relationship between the Coefficient of Friction (μ), bearing distance and moment arm distance. Rearranging Equation 12 will derive the three conditions that must be met for an application to be capable of motion. Equations 13-15 will separate the maximum allowable Coefficient of Friction (μ), the maximum allowable moment arm distance (D₁) and the minimum allowable bearing length (L₁).

Equation 13: L_1-min = 2 x μ x D₁ → L₁> 2 x μ x D₁

Equation 14: D_1-max = L₁ / (2 x μ) → D₁< L₁ / (2 x μ)

Equation 15: μ_max = L₁ / (2 x D₁) → μ< L₁/ (2 x D₁)

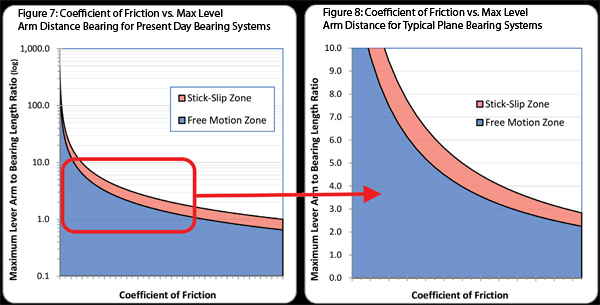
A graph can be created showing what the maximum allowable Binding Ratio would be for any coefficient of friction. Figure 7 illustrates that the smaller the coefficient of friction, the larger the Binding Ratio can be. For this figure, Equation 14 was used and the bearing length, L₁, was set to a value of L₁ = 1. The X-axis shows different values for the coefficient of friction, μ, and the Y-axis shows the Binding Ratio.

For illustration purposes, the lowest common coefficient of friction commonly found in linear motion systems today is in recirculating ball type linear guides where the coefficient of friction can be as low as μ = 0.001. Using Equation 14, and setting the bearing length to 1, the result is a Binding Ratio of 500:1. The highest coefficient of friction found in modern day plane bearings is μ = 0.5; however, most modern day materials have a value of μ = 0.1 – 0.25. Figure 7 graphically illustrates the importance of a low coefficient of friction for applications with a high moment load and a large moment arm distance.

The assumption was made that all forces are applied in an axis that is parallel to the direction of travel. This assumption eliminates the complication and redundancy of vector mathematics. In most practical applications, the force would actually be applied at some non-parallel angle, which would require the force to be broken down into its X-Axis, Y-Axis and Z-Axis vectors. The end result would be the same. The only difference is that the formulas would have to be repeated three times, once for each axis.

Stick-slip
One of the most frustrating and potentially devastating problems an engineer can face is stick-slip motion. It can bring production to a standstill until the problem is solved. While we have covered the coefficient of friction (μ) as if it was a single value, in reality, every material has two coefficients of friction: static (μs) and dynamic (μk). In general, the coefficient of static friction is greater than or equal to the coefficient of dynamic friction. This value will certainly be different for every material, so be sure to check the specific value for designed in materials.

Remember, the greater the coefficient of friction, the lower the Binding Ratio will be. Thus, the difference between the static and dynamic coefficient of friction means that there could possibly be some designs that will work when the system is already moving, but will not work when the system is at rest. Figure 7 plots the Binding Ratio for different static and dynamic coefficients of friction. Figure 8 is a detail view of Figure 7.

There are two curves plotted in each figure. The top curve represents the Binding Ratio curve based upon the static coefficient of friction. The bottom curve represents the Binding Ratio for the dynamic coefficient of friction based upon the assumption that the dynamic coefficient of friction is 35% less than the static coefficient of friction. The blue area at the bottom of the plot is the “free motion zone” where motion will not theoretically be interrupted by binding due to the Binding Ratio. The red area is the area between the curves of the Binding Ratio for the static and dynamic coefficients of friction. The white area above the curves is the “no motion” zone where it is likely that motion will not occur. Stick-slip is more likely to occur for applications where the Binding Ratio is in the red zone (the area between the curves).

Figures 7 and 8 are not meant to be used as an engineering reference chart, rather, they should be used for illustration purposes only. Linear recirculating ball based systems often have static and dynamic coefficients of friction which are almost identical, so there is little change in the binding ratio. Plane bearings typically have a larger difference between the static and dynamic coefficient of friction, so there will be a larger variance in the binding ratios.

Stick-slip is often described as a temporary cycle of alternating rest and motion. Some systems experience stick-slip motion only at certain locations during the cycle. If this type of motion is repeatedly observed at the same location, then it is likely that an unknown force is acting upon the system at that location.

The most common external forces are caused by misalignment of the linear rails, change of dimension for the rails, or an imperfection in the rail (which can also be caused by damage). These additional forces are not accounted for in Figure 5 and all of the equations here. These forces must be multiplied by the force of friction and then added to the resultant forces from the moment load. Looking back to Equation 10, it can be rewritten as Equation 16 to account for these additional forces. Provided that the applied force, F₁, is still larger than the frictional forces, then motion will still occur. However, if the sum of the frictional forces exceeds the applied force, binding will occur.

Equation 16: Acceleration = 0 → F₁ = μ (F₂ + F₃) + μ(other forces)

Since the system was likely in motion before these additional frictional forces were applied, the momentum of the system will help push through the momentary zone where these external forces are applied. As the system moves through this zone, the applied force will re-engage to cause a short burst of motion before resulting in binding again. The momentum will again help push the system through the binding where the cycle can repeat. This is stick-slip in its simplest form.

Complications, limitations and troubleshooting

By far, the largest complication for working with the Binding Ratio, is that the actual Coefficient of Friction is hard to quantify and may change based upon environmental circumstances. To further complicate matters, some manufacturers either do not list the Coefficient of Friction in their product literature or may only list the dynamic Coefficient of Friction to make their products appear more favorable. Another issue with accurately using the Binding Ratio is the additional, unaccounted and often unpredictable forces caused by misalignment. In addition, some of the more advanced bearing materials will actually have their Coefficient of Friction change based upon the load applied. A good rule of thumb is to take the expected coefficient of friction and to double it. This ensures there will be adequate safety factor within the design.

Another complication results from using the incorrect bearing length. Aside from mathematical and unit conversion errors, the most common problem is a result of using the wrong bearing length in the formulas. This is very easy to do because the bearing length is not the overall bearing length, which is the most common assumption. Instead, bearing length means the length of the bearing carrying the load. In a ball bearing system, this is typically called the “load zone.” Few manufacturers publish specifications as to the details of their load zone, so engineers have to guess a specific bearing (“load zone”) length. Another common mistake happens for applications with multiple bearings on a single shaft. The correct bearing length is the center-to-center distance between the bearings and not the overall length (outside edge to outside edge length).

There are five simple concepts that, if implemented, should solve a binding/stick-slip problem for most applications. The five simple concepts are, in no particular order:

• Reduce Moment Arm Distance
• Increase Bearing Length
• Add a Counter Balance
• Remove External Forces
• Reduce Bearing Friction

The most logical change to prevent binding would be to reduce the moment arm distance. Reducing this distance will move the application out of the binding or stick-slip zone and bring it down into the smooth motion zone (see Figures 7 and 8). This is a great concept in theory; however, this is simply not an option for most applications as other system constraints prevent this distance from changing.

The next suggested change would be to make the bearing length longer. This can be done by switching to a longer bearing/carriage, increasing the spacing between multiple bearings or adding a second bearing to a single bearing system. This may be a solution for many applications; however, not all systems can allow for a longer bearing length. In this case, the next suggestion would be to try to add a counterbalance to reduce the moment, which will reduce the resulting forces and consequently the frictional forces (Figure 5). Again, this may not work for some applications as there may not be space to add a counterweight or overall system constraints prevent the additional weight or cost of the counterweight.

A different solution would be to attempt to remove any external forces. These most often are a result of either misalignment or damage to a shaft/rail. Damaged shafts/rails may or may not be able to be fixed. They may have to be replaced to eliminate the additional forces encountered at the damaged portion.

The final suggestion would be to reduce the bearing friction. There are two primary ways to accomplish this: by adding or changing the type of lubrication to reduce the coefficient of friction or by changing the bearing type to a different style with a lower coefficient of friction.

Some applications will experience smooth motion in one direction and binding in the opposite direction. This is almost always a result of forces previously unaccounted for. Typically the forces are accounted for in one axis, but forces are seldom applied in only one axis. It only takes one axis having a force applied at a distance farther than the Binding Ratio distance to have the whole system experience stick-slip motion or complete binding. Troubleshooting this issue can be frustrating, as the system seems to work half of the time. In this case, the most commonly applied solution is to increase the bearing length, either by increasing the distance between the bearings or switching to an extended length bearing.

Reprint info >>

PBC Linear
www.pbclinear.com