It’s rare in linear motion for a guide or ball screw to carry the same load throughout its move cycle. Even in simple pick-and-place applications, the load will be higher in one direction (the pick and carry phase) than in the other direction (the place and return phase). But even more common is for a load to change multiple times, or constantly, during a cycle. A good example of this is dispensing. In dispensing applications, the stroke can start off with a range of loads, depending on how much dispense media is being carried. As the dispense media is applied and used up, the load on the bearing system decreases. And when the media is fully replenished in the dispensing system, the load is at its greatest.
We know that bearing life is dependent on the applied load, but how do you account for a load that is not consistent?
The best way to calculate bearing life with changing loads is to use the mean equivalent dynamic load on the system.
The equation for mean equivalent dynamic load looks intimidating, but it’s relatively simple, taking into account each discreet loading phase and the percentage of total travel that each load is applied during the move cycle.
For linear ball bearings:
![]()
For linear roller bearings:
![]()
Where:
Fm = mean equivalent dynamic load
F1…Fn = load during each phase
L = total travel over the move cycle
L1….Ln = distance traveled during each phase
You can see from the equation that each discreet load is multiplied by the distance traveled while that load is applied. And the entire equation is divided by the total travel. This converts the travel in each discreet phase to a percentage of the total travel. So if the application has three different loads, and the travel with F1 is 100mm, the travel with F2 is 300mm, and the travel with F3 is 100mm, then F1 is present for 20% of the travel, F2 is present for 60% of the travel, and F3 is present for 20% of the travel.
Because these equations calculate the mean dynamic load, which is used for determining bearing life, static forces, such as pressing or holding, are not included.
For ball screw assemblies, the mean equivalent dynamic load is dependent on time rather than distance, and takes into account varying speeds as well as forces. By multiplying each force by the rotational speed and time spent at that speed, then dividing by the sum of the various speeds multiplied by their times, we obtain an average of the time each load is applied versus the total cycle time of the ball screw assembly.
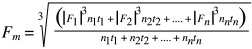
Where:
n1….nn = rotational speed during each phase
t1….tn = time spent at each rotational speed
Notice that in each of the mean equivalent dynamic load equations, the absolute value of the loads, |F|, is used. So even if the load is acting in the reverse direction, it is still added to (rather than subtracted from) the total load.
In a case such as the dispensing application mentioned above, where the force changes not just with discreet phases, but varies constantly, the accepted approximation is to take the average load during each phase. A more conservative approach would be to take the maximum load during each phase, but this could lead to significant over-sizing of the bearing system.
To decide which approach is better for a given application, consider the magnitude of the load and other safety factors that have been applied. If using the average load during each phase gives a bearing life that is borderline acceptable, recalculate the life using the maximum load during each phase, which will also allow some margin for unexpected loads or conditions.
Feature image credit: SKF


Leave a Reply
You must be logged in to post a comment.