How to calculate acceleration

Once you know which move profile is being used, you’ll need to know how to calculate acceleration based on total move distance and total move time. When sizing a linear system, a lot of attention is given to velocity, but the effects of acceleration on the system and its components are often more significant than those due to velocity.

Acceleration is most associated with the move profile and how to best achieve the required travel in the specified time, but it also causes additional forces on the system and components (recall Newton’s second law, F=ma), which must be accounted for in sizing and selection. It also plays a significant role in determining how much torque is required from the motor to drive the load.

---

Acceleration is the rate of change of velocity: change in velocity divided by change in time. In calculus terms, acceleration is the derivative of velocity (dv/dt) and can be determined by calculating the slope of the move profile (velocity vs. time) curve. 

---

The first step in calculating the required acceleration for a move is to determine what type of move profile the application will use—triangular or trapezoidal.

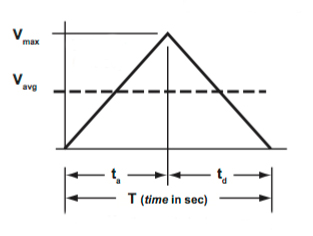
How to calculate acceleration for a triangular move profile

For a triangular move profile, acceleration is accomplished in half of the total move time and half of the total move distance. (Likewise, deceleration takes the remaining half of the move time and half of the move distance.)  So the acceleration time (t_a) equals 1/2 of the total move time:

And the acceleration distance (d_a) equals 1/2 of the total move distance.

Recall that acceleration is the rate of change of velocity, or velocity divided by time. In order to determine acceleration, we need to know the maximum velocity. For simplicity, we start by determining the average velocity.

Average velocity is simply the total move distance divided by the total move time:

For a triangular move profile, the maximum velocity is 2 times the average velocity, which can be expressed as:

Acceleration is the maximum velocity divided by the time to accelerate:

Substituting for v_max and using the equation for t_a from above:

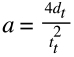
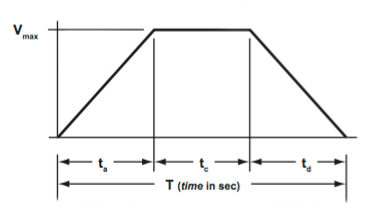
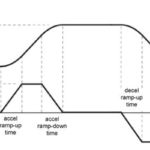
How to calculate acceleration for a trapezoidal move profile

A purely trapezoidal move profile uses 1/3 of the total move time for acceleration, 1/3 for constant velocity, and 1/3 for deceleration:

Similarly, 1/3 of the total move distance is covered during acceleration, 1/3 during constant velocity, and 1/3 during deceleration:

Like a triangular move profile, the average velocity for a triangular move profile is simply the total move distance divided by the total move time:

But the maximum velocity for a trapezoidal move profile is a bit lower than it would be for the same move executed with a triangular move profile. Instead of maximum velocity being twice (2x) the average velocity, the maximum velocity for a trapezoidal profile is only 1.5 times the average velocity. (This can be seen by analyzing the geometry of a trapezoid, as explained in this post.)

Acceleration is the maximum velocity divided by the acceleration time:

Substituting for v_max and t_a (and replacing 1.5 with the fraction, 3/2):

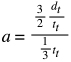
Simplifying, we get:

---