How to size a spline shaft: Shaft strength in bending and torsion

Choosing a shaft for a traditional linear ball bushing is relatively easy — choose the appropriate diameter, material, and hardness, check the dimensional accuracies and tolerances, and if the shaft is unsupported, perform a beam deflection calculation.

But because spline shafts can withstand both radial and torque loads, it’s important to ensure the shaft strength is sufficient to withstand the applied bending and torsion moments and that the torsional rigidity is sufficient to keep the twisting angle of the shaft within permissible limits.

---

Required spline shaft diameter based on bending moment

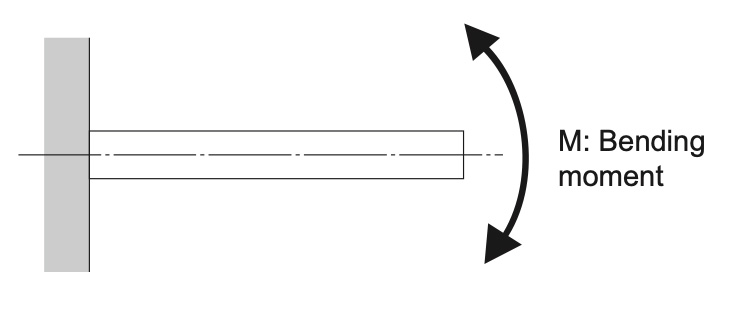
The first step in analyzing spline shaft strength is to determine the shaft diameter necessary to withstand the applied bending moment.

The maximum applied bending moment equals the allowable bending stress multiplied by the shaft’s section modulus:

M = bending moment (N*mm)

σ = maximum allowable bending stress (N/mm²)

Z = section modulus (mm³)

Most shaft manufacturers provide the section modulus for each shaft type and diameter, so by solving this equation for the section modulus, Z, the appropriate shaft diameter to withstand the applied bending moment can be selected from the manufacturer’s catalog.

Otherwise, the section modulus for a solid shaft is given as:

d = shaft diameter (mm)

To find the required shaft diameter to withstand the applied bending moment, the equation can be rewritten as: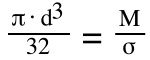

---

Required spline shaft diameter based on torsion moment

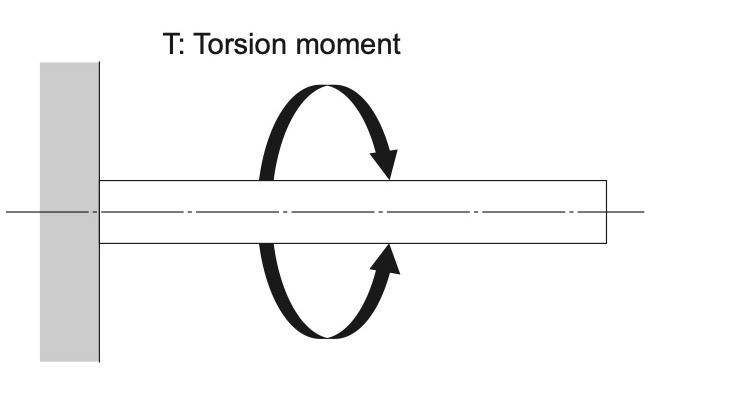
Because the spline shaft also experiences torque (twisting) loads, the shaft must have sufficient torsional strength to resist these loads.

The maximum applied torsion moment equals the allowable torsion stress multiplied by the shaft’s polar modulus:

T = torsion moment (N*mm)

τ_a = maximum allowable torsion stress (N/mm²)

Z_p = polar modulus (mm³)

As with the section modulus (Z), above, most shaft manufacturers provide the polar modulus (also referred to as the torsion modulus) for each shaft type and diameter. so by solving this equation for the polar modulus, Z_p, the appropriate shaft diameter to withstand the applied torsion moment can be selected from the manufacturer’s catalog

Otherwise, the torsion (polar) modulus for a solid shaft is equal to the polar moment of inertia divided by the shaft radius. For a solid shaft, the polar modulus is given as:

d = shaft diameter (mm)

To find the required shaft diameter to withstand the applied torsion moment, the equation can be rewritten as:

---

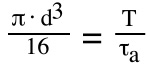
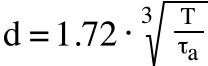
Special case: Simultaneous torsion and bending moments

It’s important to note that the cases above assume that bending and torsion moments are applied at different times. If they are applied simultaneously, the equivalent values for bending and torsional moments must be calculated, and these should be used in place of M and T in the equations above.

Equivalent bending moment:

M_e = equivalent bending moment

Equivalent torsion moment:

T_e = equivalent torsion moment

---

Torsional rigidity

Now that the shaft diameter has been selected, its torsion, or twisting, angle should be checked to ensure that it doesn’t exceed the manufacturer’s allowable limit, which is typically ¼° per meter of shaft length:

θ = torsion angle (°)

T = torsion moment (N*mm)

L = shaft length (mm)

G = shear modulus (N/mm² = 7.9 x 10⁴ N/mm² for steel shaft)

I_p = polar moment of inertia (mm⁴)

---

In addition to these calculations for shaft strength, the shaft deflection caused by radial loads should also be calculated and checked against the manufacturer’s maximum allowable value.