Coordinate systems provide a way to define a point in space in either one, two, or three dimensions.
The most prevalent coordinate system used in linear motion applications is the Cartesian system. Cartesian coordinates define a position as the linear distance from the origin in two or three mutually perpendicular axes. The origin is the point where the axes intersect, and points along the axes are specified by a pair (x, y) or triplet (x, y, z) of numbers. The Cartesian coordinate system allows both positive and negative directions (relative to the origin) to be specified in each axis. With Cartesian coordinates, each coordinate set defines a unique point in space.
The Cartesian coordinate system is also referred to as the “rectilinear coordinate system” and is a special case of curvilinear coordinates.
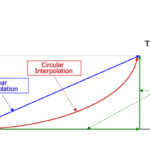
The Cartesian coordinate system is often used for straight-line movements, where specifying the motion of an axis is simple — input the location to which the axis should travel (or the amount of distance it should travel from the starting point), and it will take a linear path to the specified location. Similarly, if the application involves multiple axes, the end point is specified (x, y) or (x, y, z), and the axes can travel independently, one-by-one to the specified location, or they can travel simultaneously in a coordinated fashion using a method referred to as “linear interpolation.”
Although Cartesian coordinates are straightforward for many applications, for some types of motion it might be necessary or more efficient to work in one of the non-linear coordinate systems, such as polar or cylindrical coordinates. For example, if the motion involves circular interpolation, polar coordinates might be more convenient to work in than Cartesian coordinates.
Polar coordinates define a position in 2-D space using a combination of linear and angular units. With polar coordinates, a point is specified by a straight-line distance from a reference point (typically the origin or the center of rotation), and an angle from a reference direction (often counterclockwise from the positive X-axis). These are referred to as the radial and angular coordinates (r, θ).
Recall from above that with Cartesian coordinates, any point in space can be defined by only one set of coordinates. A key difference when using polar coordinates is that the polar system allows a theoretically infinite number of coordinate sets to describe any point. Two conditions contribute to this. First, the angular coordinate, θ can be any multiple of a full revolution (one revolution is 2π). For example, the angular locations of (5, 0), (5, 2π), and (5, 4π) are the same, as are (5, π/2) (5, 3π/2), and (5, 5π/2).
Also, the direction of rotation to find the polar coordinate can be counterclockwise (indicated by a positive (+) angle) or clockwise (indicated by a negative (-) angle), and the radial coordinate can also be positive or negative. Negative radial coordinates are used when the angular coordinate places the location in the opposite quadrant from the intended point. The negative radius moves the point back to the intended quadrant. The example below shows four coordinates that all describe the same point.
(5, π/3) = (5, -5π/3) = (-5, 4π/3) = (-5, -2π/3)
Converting between polar and Cartesian coordinate systems is relatively simple. Just take the cosine of θ to find the corresponding Cartesian x coordinate, and the sine of θ to find y.
And basic trigonometry makes it easy to determine polar coordinates from a given pair of Cartesian coordinates.
Note that there’s no conversion between Cartesian and polar coordinate systems for the z coordinate. Although Cartesian coordinates can be used in three dimensions (x, y, and z), polar coordinates only specify two dimensions (r and θ).
If a third axis, z (height), is added to polar coordinates, the coordinate system is referred to as cylindrical coordinates (r, θ, z).
Leave a Reply
You must be logged in to post a comment.