Linear bearings that use balls or rollers to carry a load are subjected to Hertz contact stresses — a type of material stress that plays a significant role in determining the bearing’s load capacity and fatigue life.

---

When two surfaces of different radii are in contact and a load is applied (even an extremely small load), a small contact area is formed, and the surfaces experience very high stresses. These stresses are known as Hertz (or Hertizian) contact stresses. In rolling element linear bearings, Hertz contact stresses occur on the balls (or cylinders) and the raceways.

In theory, the contact between two spheres occurs at a point, and the contact between two cylinders occurs as a line. In either case — point or line contact — the resulting pressure between the two surfaces would be infinite and the surfaces would experience immediate yielding. But in real-world applications, when two surfaces are pressed together with a force, some elastic deformation occurs at each surface, and a contact area is formed. The stresses that occur on the two surfaces may still be very high — sufficient to initiate spalling or other forms of failure — but they are no longer infinite.

---

The analysis of Hertzian contact stresses relies on four primary assumptions:

 – The surfaces are smooth and frictionless
 – The bodies are isotropic and elastic
 – The contact area is small relative to the sizes of the bodies in contact
 – The strains on the bodies are small and within the elastic limit

---

Hertzian stresses are present when any two surfaces with different radii are in contact — even if one surface is flat or if one surface is convex and the other is concave, which is the case for rolling element bearings: the ball or roller is convex, and the raceway is concave. In the analysis of Hertz contact stresses, a convex surface (the ball or roller) has a positive radius and the concave surface (the raceway) has a negative radius. (Note that flat surfaces have an infinite radius.)

Because the surfaces have different radii, the contact area between a spherical ball (or a cylindrical roller) and a bearing raceway has an elliptical shape. Under these conditions, the maximum pressure between the two surfaces is given as:

Spherical Ball and Raceway

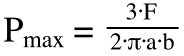
Cylindrical Roller and Raceway

---

Hertz contact stresses and linear bearings

Hertz contact stresses have a significant effect on bearing dynamic load capacity and L10 life. Shear stresses, which cause fatigue — a primary mode of failure of rolling elements — are proportional to the maximum Hertz pressure between the two bodies.

Hertz contact, and the resulting deformation of surfaces, is also what causes bearings to skid rather than roll. This is because the Hertz contact areas have different diameters than the rolling elements themselves, so the rolling elements slip. Hertz contact has implications for bearing preload as well. Preloading the rolling elements gives them a larger — and finite — Hertz contact area, which increases stiffness. But the increased contact results in high heat generation.

This is why a preload amount of just 8 percent is considered high preload for linear bearings, with preload greater than 10 to 15 percent being extremely rare. Also, because Hertz contact is non-linear, a small amount of preload can provide a significant increase in stiffness, without resulting in unacceptable slip, friction, and heat.

Feature image credit: L.C. Brezeanu